This is number 4 in my series of lectures in music technology and ChucK to the Oxford Laptop Orchestra. Delivered on the 5th of November 2012 at the Faculty of Music. Give the first three a read before reading this.
The content is complete here (except for a bit about Nyquist) so feel free to read this. But I intend to do a bit of copy-editing, and include sound samples before I declare it complete.
This week we look at low frequency oscillators, using them to modulate other oscillators and in the process how to do more than thing at once._
_
Lecture 4 — Modulation
Slowing Things Down
We’ve been playing around with oscillators and connecting them directly to the DAC and hearing the sound they produce. Last week we also discovered that ChucK stores frequencies as float numbers, not int numbers, which means we can oscillate less than one time per second.
There are lots of natural phenomena that involve oscillation at a slower speed. The crash of waves on a beach, the turning of the earth, the change of the seasons. These can all be measured in terms of cycles per second, even if those are very low factional numbers. If we open up a piano, we can start to feel the vibration of the lowest notes as a physical vibration rather than a sound. There’s a wide continuum of oscillation speed, from once a year to once a day to once a second to ten times a second to a thousand times a second.
Here’s a ChucK program which creates an oscillator, connects it to the DAC. It then runs a for loop, starting i at 400 and reducing it down to 1 Hz, little by little. Note that I’m using a float as my loop variable, and I’m decreasing, not increasing the value. If you can listen to this on big speakers you have a better chance of hearing lower pitches.
SinOsc osc;
osc => dac;
float i;
for (400.0 => i; i > 1.0; i - 1 => i)
{
i => osc.freq;
0.05::second => now;
}
That’s dropping 1 Hz every 0.05 seconds. Here’s a picture.
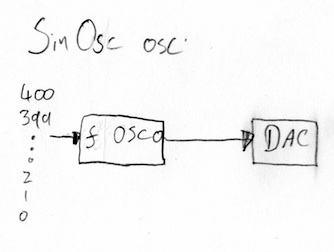
If we had a big speaker that we could see, it would eventually get the point where we could see it moving back and forth.
Hearing the Low Frequency Oscillation
Last week we heard heard about using a control voltage to control an oscillator. Early synthesisers had a number of inputs (let’s say one for the frequency and one for the amplitude). If you got hold of a fader you could plug it into the frequency input and create swooping frequency gissandi. If you attached it to the amplitude input you could vary the volume of the oscillator. You could also get a keyboard which produced a control voltage and use that to ‘play’ the oscillator by connecting it to the frequency input.
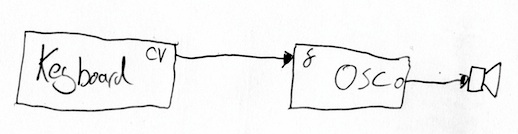
But there is one more piece of equipment in our virtual synthesiser laboratory that can produce interesting voltage outputs: another oscillator.
An oscillator takes control voltages as inputs and produces a changing voltage as an output. We can, therefore, take an oscillator running at a low frequency and plug it into the amplitude of a second. The result is an oscillator that grows louder and quieter.
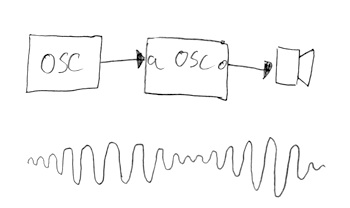
When we use an oscillator like this, it is called an LFO, or Low Frequency Oscillator.
- Listen to nearly any music track made with electronics.
- Listen for a periodic change in the sound.
- Declare ‘that’s an LFO!’
- Earn respect and notoriety from your peers.
Let’s try and do some amplitude modulation in ChucK.
Not so Fast
ChucK has a brilliant syntax for plumbing things together, the ‘chuck operator’, spelled ‘=>’. It works for certain kinds of types, but we can’t just chuck the output of one oscillator to another. It doesn’t quite work like that.
We’re going to have to do this ourselves. What we want to do is set up two oscillators and then keep a watch on one of them and use that value to modulate the other one. This will require a loop in which we continually observe the LFO and make changes to the other oscillator.
First of all I’m going to set up an LFO. I’m not going to chuck it to the dac, because we don’t actually want to hear the output, we want to use it for our own means. You’re probably used to seeing ‘osc => dac;’ wherever you see an oscillator variable declared, but that’s not going to happen here. For this step, I’m going to print out the value of the LFO just to check that things work.
The job of an oscillator is have an output, and to make sure it oscillates. We can get the value of that output at any point in time by asking it what it’s most recent value was. The function that does it for us is called ‘last()’, and it returns to us the last value of the oscillator. So here we go:
SinOsc myLfo;
0.25 => myLfo.freq;
while (true)
{
<<< myLfo.last() >>>;
0.001::second => now;
}
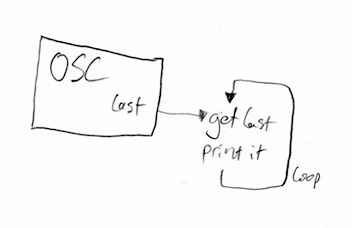
I want a loop, but I’m not going to be counting anything. I just want something that runs continuously until we kill it. Let me introduce you to the while loop. It keeps looping just as long as the expression in the brackets holds true. We’ve tricked it by giving it an expression that is always true (that is, writing true in there literally). I could have written while(1 == 1) or while(10 < 100) and it would have the same effect. I’m also going to pause a little each loop because it’s bad computer husbandry to have a loop blindingly repeating at high speed. Also we don’t care about printing the value at every available point in time, a pause of 0.001 second is acceptable.
When we run this what do we see printed out? Lots if 0.000s. The oscillator isn’t doing anything. Why?
Black Holes
ChucK is used to seeing you chucking oscillators directly to the DAC, or to other objects and ultimately to the DAC. As far as it’s concerned, there’s no point having an oscillator at all if it doesn’t somehow end up coming out of your speakers.
That’s not an unreasonable assumption. It costs computer power to keen an oscillator ticking over. Imagine if you created a million oscillators as part of your program but you only connected 5. You might disconnect then and connect a different 5 later on. There would be no point keeping the unconnected oscillators ticking over when it knew for a fact that you weren’t listening to them.
We may not be listening to the LFO oscillator, but we still want it to run, as we’re interested in getting the values out. We need a way of telling ChucK ‘look, trust me. I know I’m not listening to this oscillator but I still want it to run’. This is calle the black hole. It’s an output, like the dac output, except the signal that you send into it disappears into nothingness. If an oscillator is connected to it, that’s a signal to ChucK that it should keep the oscillator running and you have your own reasons.
So I’m going to chuck the LFO to the black hole and run the program again.
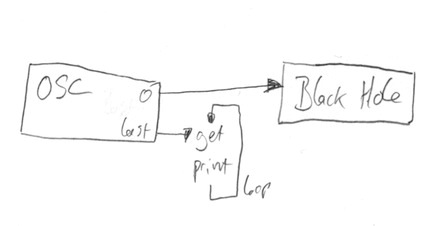
SinOsc myLfo;
0.25 => myLfo.freq;
myLfo => blackhole;
while (true)
{
<<< myLfo.last() >>>;
0.001::second => now;
}
And there we have it. Lots of numbers that look something like this:
0.827101 : (float)
0.826219 : (float)
0.825335 : (float)
0.824449 : (float)
0.823561 : (float)
They range from -1, through 0 and up to 1. And back. We can see the numbers that our oscillator is producing. I’m going to show you again the chart of the output of a sine wave oscillator.

Modulating Amplitude
We can use this to modulate the amplitude of another oscillator. But first we need to do a bit of arithmetic.
The amplitude input is expected to be between 0 and 1. Zero is volume turned right down, 1 is volume turned right up. Internally, ChucK just needs to multiply the signal by the amplitude to apply the volume value. Multiply by 1 and you get the same number, multiply by zero and you get zero. Multiply by 0.5 and you get half the signal.
Our LFO is going to merrily produce values between -1 and 1. To make this usable, we need to turn that into between 0 and 1. So we add 1 to the output : (so it’s beween 1 and 2) and then divide by 2. I’m just going to modify our program to print the numbers between 0 and 1:
SinOsc myLfo;
0.25 => myLfo.freq;
myLfo => blackhole;
while (true)
{
<<< (myLfo.last() + 1) / 2 >>>;
0.001::second => now;
}
Run it and see what happens. You’ll see the numbers between 0 and 1.
Notice the brackets there. If we wrote x + 1 / 2 that might be a bit ambiguous. The programming language has rules built in which means that the divide is applied before the add. So we need to add brackets to make our intention clear (and correctly do what we want).
Time for action. Instead of printing the value I am going to assign it to the gain (aka volume control) of a second oscillator.
SinOsc osc;
osc => dac;
400 => osc.freq;
SinOsc lfo;
0.5 => lfo.freq;
lfo => blackhole;
float theValue;
while (true)
{
lfo.last() => theValue;
(theValue + 1) / 2 => theValue;
theValue => osc.gain;
0.001 :: second => now;
}
You’ll notice that I’ve set 0.5 Hz as the LFO value because why not. Play with it yourself.
Vibrato
Let’s make some vibrato. Vibrato means playing a note, and wobbling the frequency above and below. Lucky our LFO gives positive and negative numbers. I’m going to use a TriOsc for my ‘sound’ oscillator just for a change of scene. I’m going to use a SinOsc for my vibrato oscillator.
I need to pick a frequency to play, and then add the vibrato LFO value (which may be positive or negative). Adding or subtracting 1 Hz either way isn’t going to make much difference, so I’m going to try multiplying it by 20 (so the output is a range of -20 to 20) and then add to the frequency I wanted.
TriOsc osc;
osc => dac;
400 => osc.freq;
SinOsc vib;
vib => blackhole;
7 => vib.freq;
int myFreq;
440 => myFreq;
float theValue;
while (true)
{
(vib.last() * 20) + myFreq => osc.freq;
0.001 :: second => now;
}
10 :: second => now;
Of course it should be a bit more subtle than that. Experiment with the frequency of the LFO (vibrato speed), the value you multiply by (vibrato amount) and the oscillator you use for it. The Sawtooth Oscillator, SawOsc is particularly horrific.
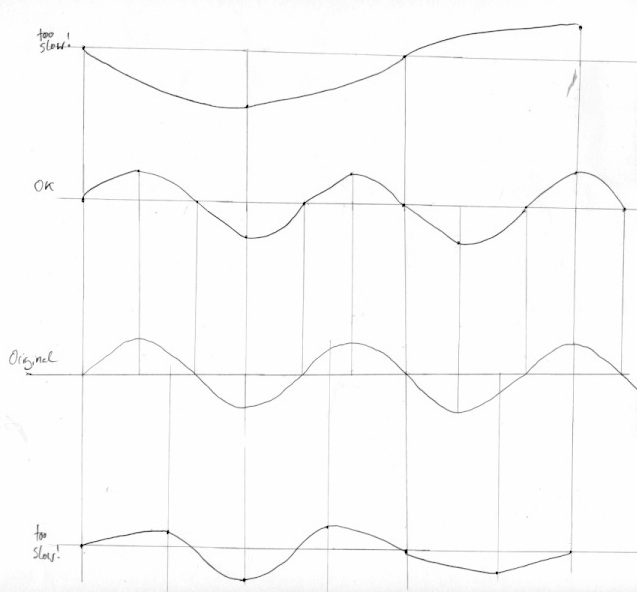
Nyquist’s Theorem
We need to be very careful about how our LFO ‘pump’ operates. In order to be a good citizen we need a bit of a pause in the loop, or we’ll lock up ChucK. But if the pause between iterations of the loop is too long then we’re going to get odd results from the LFO. TODO : MORE TO FOLLOW.
Doing JS Bach a Great Disservice
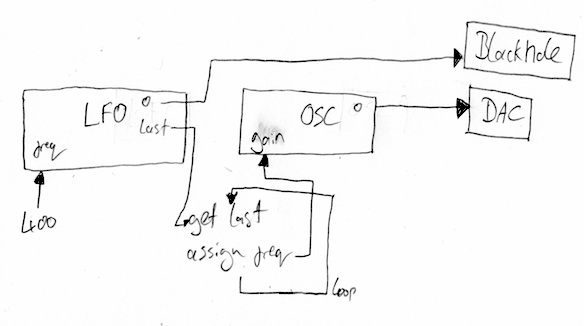
Now I’m going to take advantage of all of we’ve learned so far. I’m going to take last week’s _Jesu Joy of Man’s Desiring _player. Remember that uses an array of SinOscs, one for each rank of ‘pipes’. I’m then going to make another array of SinOscs, but this time use then as LFOs. Each one will have a slightly different frequency, so they will be out of sync.
I will then use each LFO to adjust the position of its corresponding ‘pipe’ oscillator in space. I will pan each oscillator from left to right. The input for pan is a float between -1 (hard left), 0 (centre) to 1 (right). By happy co-incidence that means that I can use the output of the LFO directly.
One spanner in the works is that each oscillator is mono (a single channel) not stereo (two channels). We need to convert the signal into a stereo signal before being able to pan it. Let me introduce Pan2. This will take a mono sound input from an oscillator, and produce a stereo output. It will also allow us to control the pan. So another array, this time a load of _Pan2_s, one for each oscillator.
Here’s a picture of what will be happening, connection wise.
Time to Spork
We need a function to pump our LFO values. So far we’ve just applied it to an oscillator doing nothing, but our music code is actually doing something (looping over the array). We need to do two things at once.
For this we need a function that will run in the background (in this case our LFO pump). We can then ‘spork’ the function. This means calling the function as normal. When we call a function normally, the code calling it waits for the function to complete. When we spork it, the function runs but the rest of the program keeps running. Thus ChucK is able to do more than one thing at once.
I’ll jump right in. Here is the full program, with comments. Look out for the spork!
``
// Create five SinOscs to make the sound.
SinOsc oscs[5];
// Create five SinOscs to be LFOs.
SinOsc lfos[5];
// Create five Pan2s, which we will use to pan each sound producing SinOsc.
Pan2 pans[5];
// Assign low frequencies, one to each LFO.
1 => lfos[0].freq;
0.2 => lfos[1].freq;
0.4 => lfos[2].freq;
0.6 => lfos[3].freq;
0.8 => lfos[4].freq;
// Loop through five times (oscs is five long as are the others).
int i;
for (0 => i; i < oscs.size(); i++) {
// For each, connect oscillator i to Pan2 i.
oscs[i] => pans[i];
// Connect Pan2 i to the dac.
pans[i] => dac;
// Connect the LFO to the black hole so it runs.
lfos[i] => blackhole;
}
// Now define a load of variables, one for each pitch we want to use.
float D, E, F, Fs, G, A, B, c, d, e, f, fs, g, a, b;
// Assign the MIDI pitches for each pitch.
62 => D;
64 => E;
65 => F;
66 => Fs;
67 => G;
69 => A;
71 => B;
72 => c;
74 => d;
76 => e;
77 => f;
78 => fs;
79 => g;
81 => a;
83 => b;
// Create an array of pitches which we'll store our tune in.
float pitches[];
// Here's the tune, written in terms of the variables holding MIDI pitches.
[G,A, B,d,c, c,e,d,d,g,fs, g,d,B, G,A,B,c,d,e, d,c,B, A,B,G,Fs,G,A, D,Fs,A, c,B,A,B,G,A, B,d,c, c,e,d, d,g,fs, g,d,B, G,A,B, A,d,c, B,A,G, D,G,Fs, G,B,d, g,d,B, G] @=> pitches;
// Here's a function which will take the frequency
// and assign it to each SinOSc with the right multiplication to make a pipe sound.
function void assignFrequency(float frequency)
{
frequency / 4 => oscs[0].freq;
frequency / 2 => oscs[1].freq;
frequency * 1 => oscs[2].freq;
frequency * 2 => oscs[3].freq;
frequency * 4 => oscs[4].freq;
}
// Here's a void function. This pumps the LFO value to the pan.
function void spin()
{
// Go forever.
while (true)
{
// Loop variable j.
int j;
// Loop from 0 to the number of LFOs (five).
for (0 => j; j < lfos.size(); j++)
{
// Take the last value of LFO j and assign it to the pan of Pan2 j.
lfos[j].last() => pans[j].pan;
}
// Pause a little in each loop.
0.001 :: second => now;
}
}
// Run the fuction spin in the background by sporking it.
spork ~ spin();
// It'll now run continually until our program exits.
// Now we have the music player.
// Loop from zero to the size of the pitch array.
for (0 => i; i < pitches.size(); i++)
{
// Get the actual frequency of the MIDI note at that position.
float frequency;
Std.mtof(pitches[i]) => frequency;
// Call assignFrequency to set the frequencies in the various oscillators.
assignFrequency(frequency);
// Pause quarter of a second each loop.
0.25 :: second => now;
}