This is number 3 in my series of lectures in music technology and ChucK to the Oxford Laptop Orchestra. Read the other two first. Sorry this blog post was a couple of weeks late. It’s quite substantial, but conceptually it underpins a lot of material. Persevere, read, ask questions.
This week sees a bit of a philosophical turn as we contemplate what ‘digital’ really means and how we can use it to play Bach on organ without having to build one first.
Lecture 3 : Transcending Analogue
‘Transcending Analogue’? What a ridiculous title. Surely there’s a better one. I’ve had a think and I’m not sure there is, given the subject matter. We talked before about what analogue and digital mean and what the implications of the two ways of doing things is. Today we’re going to look at them on a more fundamental level and, in the process, find out more about ChucK.
Reality Check
We live in an analogue world. What does that mean exactly? Let’s suppose I have an apple in my hand. We’re thinking about representational systems here, and we have to come up with a system to represent the number of apples I have. The most obvious way of representing that fact is the apple itself. I can show it to you, and you can see that I have an apple. If I want to record for posterity how many apples I had today, I could hold onto it indefinitely, but that would negate somewhat the point of having the apple. Who cares how many apples I have if I can’t eat them?
Comparing Apples and OrangesWater
So I get another apple, and I put that in a drawer. That one apple corresponds to my own apple. If I took out a knife and gave half my apple to someone, I could also chop the ‘representational’ apple in half and I would still have a valid representation of my worldly goods at that point in time.
Let’s also say that I have a glass of water. Again, the best way of representing how much water I have is by getting another glass and filling it the same amount.
Here I have two kinds of information : one is the number of apples and one is the amount of water. Even though I am able to chop the representational apple in half I am still measuring the **number **of apples. These are counting numbers, numbers used to count things. If I were talking about stones, which aren’t splittable, then I’d be using integer counting numbers. If I’m talking about apples, which can be split, I’m talking fractional numbers.
The amount of water, though, that’s a bit different. True, I have a glass of it, but I’m only using this size glass because of the amount of water I have. If I suddenly found a lot more water, I could upgrade to a larger glass. To measure amount of water I have I can use units, such as ‘glassworths’, but it’s a continual value. There’s nothing about water that means I have to measure it in glasses worth, whereas there is something about apples that means I have to measure it in applesworths, however I decide to store that measurement.
Keeping Things in Proportion
If I drink part of my glass of water I can make a change in my representational medium, and that will again represent the amount of water I have. This should be ringing bells about the definition of analogue, where the medium of representation changes in proportion to the thing I’m representing.
In proportion? Yes. I can store half the amount of water, and as long as I know that I need to multiply by two whenever I look at it to understand how much water it represents, that’s fine.

Of course, I don’t need to store water and apples to represent how much water and how many apples I have. I can cut a piece of string or make a mark on a piece of paper to represent how much water, or draw a series of little bar-charts to represent how many apples, each bar being analogous an apple. A full bar is a whole apple, half a bar is half an apple. If the string shrinks, or if the line on the piece of paper got smudged, or if my hand slipped when drawing the charts, I’d end up representing the wrong value.
This is the analogue world. Everything is real. Every object exists in the physical world, and, if you want to make a representation of it, so must the representation.
The Facts of Life
Which is a shame for the early pioneers of sound synthesis.
An analogue electronic synthesiser is an analogue representation of a physical oscillator, such as a tuning fork or a string. It represents the position of the tine of the tuning fork, as a proportional voltage, in the same way that a piece of string can represent the quantity of water. It also represents the behaviour of the oscillator. More on that later.
Consider the poor souls who pioneered the first analogue synthesisers. If they wanted an oscillator to make a sound, they had to go out and buy the components and make one. These were big beasts. If they wanted two, they’d have to procure a second one. If they wanted a thousand they’d have to have serious words with their funders, who would be paying not only for a thousand oscillators, but probably a new building to put them in too. The same is not true of us today.
Why?
If it Walks like an Apple, Talks Like an Apple…
I’ve said ‘here’s a variable, and it’s of type integer’ and you’ve nodded and, I hope frowned. What does the word type actually mean?
A type is an understood way of representing information, coupled with a set of things we can do to that representation, essentially, how that representation can behave. A way of writing something down on, for example, paper (or in computer memory), and a set of verbs that we can apply to our representation.
We’ve talked about three types of ‘real thing’ here.
How do you represent a quantity of apples on paper? You take apples from the pile, one by one. Each one you remove you make a mark on a piece of paper. If it’s a complete apple you fill the box in completely. If it’s half an apple you fill the box in half. And so on.
How does an apple behave? An odd question, apples don’t really behave. If we talking about the system of representation, though, the way we represent how many apples we have, there are some things we can say. One by one, I can cross off apple-boxes on piece of paper A and add them to piece of paper B. If I have an incomplete box and an apple to add, I can fill the remainder of the incomplete box up and then write down the remained of the apple I used to partially fill that box. I have to be careful doing this, because if I over or under filled the box, my representation would become inaccurate.
Same for pieces of string. I can attach them together, end to end, to add values together. Subtraction is possible, too, I just need to cut some off.
What’s the difference between a glass of water and a tuning fork?
A tuning fork has a measurement that we can take, much like a glass of water. That measurement is ‘how far from the rest position are the tines?’. The difference is that we also have the time domain to think about. The amount of water in a glass stays pretty much constant. A tuning fork’s value changes many times a second. We have drawn charts to represent this on paper, with the time domain on the x axis and the position from centre on the y.

But we want to model the behaviour and reproduce it rather than just make observations. We can’t do that on paper. We need to get electronics involved.
This is an oscillator. We’re still talking analogue. There is a voltage which rises and falls in the same way that the tine would move back and forth.
Making a saw-tooth oscillator
Through some sleight of hand I’m going to switch to a saw-tooth oscillator because it’s easier to describe. In order to make one, we need to describe the rules by which it behaves. This is easy.

- Over time, increase the output voltage by a bit
- If the voltage reaches a certain value, reset it back to zero
Simple.<
Type = Data + Behaviour
So we have three types. The first two are fractional numbers, used in two different contexts, and the third is a sawtooth oscillator. If you can represent something as a type, you can represent it in a computer system.
The oscillator is made up of two pieces of information, the time and the current output. They are both fractional numbers. We can’t represent the oscillator type in a computer unless we can represent the types that it consists of.
I’ve been a bit disingenuous in lumping these three together. In the case of the first two I’m talking about how you represent quantity, in the second, I’m talking about an object that does things. But they all boil down to a representation of a physical phenomenon.
Computer memory is a bank of boxes waiting to hold data. Think of it like a piece of squared paper. There’s nothing fundamentally meaningful about these boxes. It’s up to a type to describe how to store information, and what you can do with that information. As long as you can describe the kind of information you want to represent and how it behaves you can store things in memory.
The definition of type is
- a way of encoding the given kind information in that memory
- instructions to say how it can behave
Computers come with a few types baked in because they would be useless without them. Languages such as ChucK come with a few more as a part of the language. And you can define your own, although you can make a lot of headway without having to.
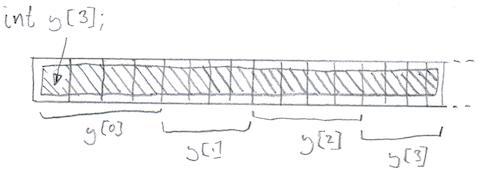
I’m going to go back to the type called ‘integer’ (or ‘int’ for short). This needs four cells to represent a number. As a part of the definition of the type, the computer knows how to encode a number in these memory cells. It also knows what to do if I ask it to add two ints together. Ditto for all the operations on integers you can think of.

The same goes for fractional numbers. These are called float. This is short for ‘floating point’, which means that you can represent a number with a decimal point anywhere (this is a historical quirk; in older systems you had fixed-point fractional numbers where you could only represent numbers in a certain range).
The same goes for any other type that you can represent, including an oscillator. The type of an oscillator requires two numbers and some instructions about how to behave through the passage of time.
When I write these:
int i;
float j;
TriOsc k;
They are all doing the same thing: setting aside enough memory to store the information required to store the type in question and connecting it with the the variable name you chose.
We have made a jump between needing to actually have the item in reality (an apple, some water, and a tuning fork that oscillates when you twang it), to an analogue way of representing it (marks on paper, string, and an electronic analogue oscillator). If we want to represent more than one we still have to physcially have more of the medium to represent it. The next jump is the exciting bit. If we have a large bank of memory going spare, and a way of representing an oscillator, we can suddenly make a thousand of them. We need to worry about how much memory we need rather than how much physical space we have. We can make a more complicated oscillator which requires more storage space, and we have fewer of them. Or simpler ones, and we can have more. Once we can describe an analogue thing and how it behaves, and once we can represent that type in a computer, we can suddenly start doing things that are absolutely not possible in reality.
Scaling Up
Let’s say we have a piece of cable. We can either send one audio signal down it (like a mic or speaker cable) or we can encode the analogue values as digital numbers and send those down the wire. If we send the numbers fast enough we can then send more than one signal down it. If we need to send even more stuff down it, we can speed up the rate of sending data. Or we could choose a type that takes up less space, even if it loses a little quality, but that allows us to send more down the cable simultaneously. This is how you can get thousands of simultaneous telephone conversations down a single cable.
The biggest problem with real things in the real world is that they need to to be real, and that can be a right old hassle. Once the things leave the analogue realm and enter the digital realm, they don’t need to be real. If you can represent it, you can do it. Once you transcend the shackles of analogue into the digital domain, the gloves are off.
The Ceremonial Removing of the Gloves
No idle boast. Let’s make ourselves a dozen oscillators.
SinOsc a;
SinOsc b;
SinOsc c;
SinOsc d;
SinOsc e;
SinOsc f;
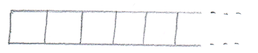
Actually let’s not do it like that. We could, but what if we want to add more later? We talked in the first lecture about representing repeated items a bit more intelligently than copying and pasting. What we want is an array. An array is way of saying ‘I want a number of slots of the same type, give me a chunk of memory’. We can ask for a dozen oscillators. Or a hundred integers. Or a million floats. Or any number of any type, so long as there’s enough memory (there usually is unless you get ridiculous).
The syntax for an array of integers is this:
int x[5];
That means ‘give me 5 integers’.
float myFloats[10];
That means ‘give me 10 floats’.
Or this:
SinOsc myOscs[12];
That means ‘give me a dozen oscillators’. When I put any of these in my program, ChucK will reserve enough space to represent that many of that type, and set them up ready for use.
Using Arrays
What do I do with them once I have them? I have some syntax, called ‘index’ which gives me the given element. We start counting at zero, not one, so the ‘zeroth’ is the first, the ‘oneth’ is the second, the ‘twoth’ is the third. It can get annoying to switch between, so I’m just going to say ‘element zero’.
int x[5];
100 => x[0];
<<< x[0] >>>;
This creates an array of ten integers, assigns the value 100 to the zeroth element. The last line prints out to the console (print meaning show on the screen) the thing you asked for. This will then print the number 100, because that’s what we stored at element zero.
For loops are natural bedfellows of arrays. If we want to find out how large our array is, we can use the size function like this:
<<< x.size() >>>;
Which will print 5, because it’s 5 long. We’ll come to functions in a bit.
So let’s create an array of ints, assign the number 8 to each element. Then we’re going to check this worked by printing the array.
int myArray[5];
int i;
for (0 => i; i < myArray.size(); i++)
{
8 => myArray[i];
}
for (0 => i; i < myArray.size(); i++)
{
<<< myArray[i] >>>;
}
A new bit of syntax for you. When I write i++ it’s the same as i + 1 => i. It has the effect of adding one to the value of the variable i. It’s something that you’ll do a lot so there’s a shortcut in the language to do that.
We saw that we can index an array by a number, but we can also index an array by a variable that represents a number. Our for loop took the value of i from zero to five (as that’s the size of the array), and each iteration of the loop, we assigned the value 8 to the element at position i.
The next loop did the same thing, except instead of assigning to element i of myArray, it printed the value.
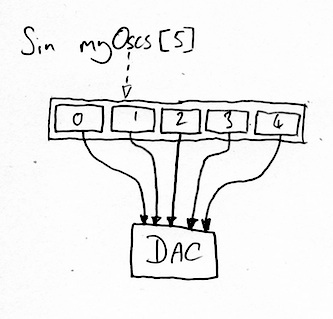
Five SinOscs Oscing
It follows that we should be able to do this with SinOscs. Remember that there’s no point having an oscillator without connecting it to the output, so we’re going to need to chuck the oscillator to the dac.
SinOsc myOscs[5];
int i;
for (0 => i; i < myOscs.size(); i++)
{
myOscs[i] => dac;
}
1::second => now;
Remember also that the ChucK program will exit immediately, so we need to pause for a second to hear the result.
It’s not all that inspiring, having five SinOscs all playing the same note. Let’s take a frequency, say 200 to be interesting (I’m sure you’re bored of 400 Hz), and then multiply that by i. So we get 200 * 0, 200 * 1, 200 * 2 etc.
SinOsc myOscs[5];
int i;
for (0 => i; i < myOscs.size(); i++)
{
i * 200 => myOscs[i].freq;
myOscs[i] => dac;
}
1::second => now;
That makes an interesting sound. Turn up the pause, listen to it. It’s not the sound of 5 sine waves (well, it is). It’s a particular timbre, made up of 5 sine waves.
There’s your first additive synthesiser. It makes a timbre. Experiment with the numbers a bit.
Let’s make some music with it!
Except to do this, we’re going to need a quick history lesson.
A Quick History Lesson
The year is many-years-ago. People are experimenting in the exciting field of making electronic music. Every oscillator ships with a keyboard built-in. The keyboard connects directly to the oscillator. This becomes a bit annoying, as you can only play one at once. Why splash out for a new keyboard every time?
So we have keyboards that can plug into any synthesiser. The keyboard produces a voltage in a wire. A low voltage means a low note, a high voltate means a high note. You can then plug this wire into any oscillator that accepts this input, called a control voltage and play any synth with any keyboard! Or any device that can produce control voltage.
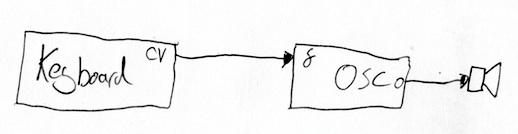
Except what does the control voltage mean? There’s some analogous proportional representation going on there, but different equipment does it differently. Is there a direct linear relationship or is it logarithmic? Does the voltage go up to 1 or 2 volts? Interconnecting equipment becomes a problem.
We need an alternative to proportional representation. And we’re not talking voting systems.
Enter MIDI, the Musical Instrument Digital Interface. You’ve probably come across it. It was designed to replace control voltages. It is a digital system for sending musical information from A to B. Because it’s digital we can represent all kinds of information, from the key you pressed, to the velocity with which you hit it, to what instrument you want and what you’re up to with the pitch wheel.
It established a digital representation of pitches on the keyboard. It was designed to fit into one slot of memory (one byte). Memory was expensive and the speed with which data was sent was slow in those days, so they tried to fit it in as small a space as possible. It turns out that 128, which is the number of values you can store in a seven bits of a one-byte integer (if you use one of the bits for something else), is also very close to the number of keys you have on a keyboard.
So MIDI pitch is a number between 0 and 127. Add 1 and you add a semitone. 60 is middle C, 61 is C# and so on. It’s a standard and convenient way of writing pitches.
History lesson over.
The Value of Functions
We’ve written tunes before. We put the frequencies in by hand. There’s nothing intrinsic about 440 Hz that says it’s an A. It happens to be an A, but only whilst we’re tuned to A = 440 tuning. When I write out a tune I’m interested in the pitches rather than the frequencies. We’re about to make a tune-playing machine, and I’m going to write MIDI pitches rather than frequencies.
We still need to give frequencies to oscillators though. So we need a way of turning a MIDI pitch into a frequency. ChucK gives us this.
We’ve written a function before. It looked something like:
function void myFunction()
We used our function to do some work for us. A function is also able to return a value. Sometimes we don’t want that, because the important thing is the work the function does for us. We have a special type for that purpose, it’s called void. When a function has the type void, it doesn’t return a value.
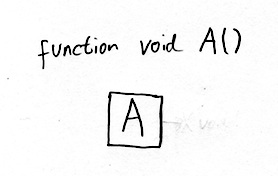
You will have come across functions in maths. The simplest function I can think of is ‘add one’. The type of that function might be int. A function can also take parameters as variables.
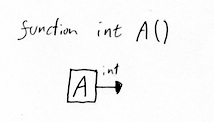

A function to add one to a number might look like this.
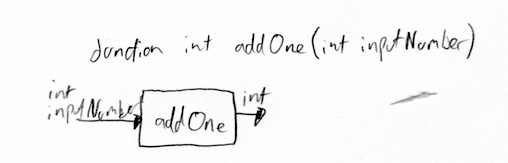
function int addOne(int inputNumber)
{
return inputNumber + 1;
}
What’s going on here? First up, the return type is int rather than void, so we know the function gives us something back. Next we see the argument. We know this syntax from variables. It’s a variable called _inputNumber _and it’s of type int.
Inside the braces we see the keyword return. That means the expression that follows it is given back to the person calling the function. In this case, we’re adding one to the number and returning that value. We might use this function:
int first;
5 => first;
int theResult;
addOne(first) => theResult;
<<< theResult >>>;
The result of this would be printing the number 6. It won’t have changed the variable first.
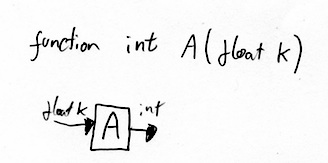
Back to MIDI. ChucK has a function called Std.MtoF. It takes a MIDI input pitch and gives us back a frequency. The type of the function is float.
Why represent a frequency as a float rather than an integer? It’s like our apples. We’re counting specific things (number of cycles per second). But there may be less than one a second. There’s a huge chasm between 1 and 0 for integer numbers. So it makes sense to store it as a float.
But the input, the MIDI pitch is also a float. In the MIDI standard it is most certainly an integer not a float. You can’t press notes between keys. And even if MIDI did allow this, it has the pitch bend. The reason why is because we can. ChucK is for experimental music, not designed for JS Bach, and why not. You can put in integers and it’ll work as expected. You can put in floats and it’ll also work, and you have a finer degree of control.
So, to use Std.MtoF:
int myPitch = 60;
int frequency;
Std.MtoF(myPitch) => frequency;
<<< frequency >>>;
The result will be the frequency of middle-C.
Man’s Desiring
We have all the pieces for a music player. We want to store a series of pitches, an array is the best thing for that. We know how to loop over the array, whatever size it is. We have a sensible way of describing pitches and a way to turn them into frequencies. We have, from week 1, known how to make a noise.
I don’t want to get bogged down with duration, so I want a tune that has notes of equal duration. And that sounds suitably pleasant. ChucK may not be designed for JS Bach but it’s not a bad vehicle.
So first up we need an array of pitches. We saw this syntax earlier:
int x[5];
20 => x[3];
That’s all very well and good, it’ll give us five _int_s. But we’re going to want to pre-load them with data and it’s going to be boring writing out line after line. So here’s some new syntax. It will create a ready-made array in memory with the values we specify.
int x[];
[1,2,3,4] @=> x;
When we write x5 it will create an array of length 5. When we write x[] it won’t create the array just yet, because we haven’t said how long we want it to be. The line immediately after creates the array and assigns it to x. Note the @=> sign, which we shall leave as necessary, but a mystery for now.
I’m not going to write the MIDI pitches directly into my array because that would get very boring very fast, and hard to fix typos. Instead I’m going to start with declaring a load of variables. Each variable will have the same name as the note, and will store the MIDI pitch in question.
int D, E, F, Fs, G, A, B, c, d, e, f, fs, g, a, b;
62 => D;
64 => E;
65 => F;
66 => Fs;
67 => G;
69 => A;
71 => B;
72 => c;
74 => d;
76 => e;
77 => f;
78 => fs;
79 => g;
81 => a;
83 => b;
Now I can write fs and know I get an F sharp, which is MIDI pitch 78.
Now I’m going to create an array with those variables.
int pitches[];
[G,A, B,d,c, c,e,d,d,g,fs, g,d,B, G,A,B,c,d,e, d,c,B, A,B,G,Fs,G,A, D,Fs,A, c,B,A,B,G,A, B,d,c, c,e,d, d,g,fs, g,d,B, G,A,B, A,d,c, B,A,G, D,G,Fs, G,B,d, g,d,B, G] @=> pitches;
I used spaces to group bars together for legibility.
Now I want an oscillator. Sine waves are so last week. Let’s use a triangle.
TriOsc osc;
osc => dac;
Now we loop along the array, using an index variable i, as it goes from zero, the first element, to the last. Each time round the loop, we get the pitch at that index, convert it to the frequency, assign it to the frequency input of the oscillator, and then pause for a quarter of a second.
Here is the complete program.
int pitches[];
int D, E, F, Fs, G, A, B, c, d, e, f, fs, g, a, b;
62 => D;
64 => E;
65 => F;
66 => Fs;
67 => G;
69 => A;
71 => B;
72 => c;
74 => d;
76 => e;
77 => f;
78 => fs;
79 => g;
81 => a;
83 => b;
[G,A, B,d,c, c,e,d,d,g,fs, g,d,B, G,A,B,c,d,e, d,c,B, A,B,G,Fs,G,A, D,Fs,A, c,B,A,B,G,A, B,d,c, c,e,d, d,g,fs, g,d,B, G,A,B, A,d,c, B,A,G, D,G,Fs, G,B,d, g,d,B, G] @=> pitches;
TriOsc osc;
osc => dac;
int i;
for (0 => i; i < pitches.size(); i+1 => i)
{
Std.mtof(pitches[i]) => osc.freq;
0.25 :: second => now;
}
Pipe Organ
We can see the effects of the the analogue reality of actually having to make things. We have had additive synthesis, where you add different frequencies together to achieve a timbre, for centuries. Pipe organs. Pipe organs are testament to two facts:
- Additive synthesis works
- If you want a lot of oscillators, you need a big building
The way that pipe organs work is by having a set of pipes that correspond to a given octave. They are described by the longest tube in the set. 8ft is standard. The lowest note on the keyboard is represented by an 8 foot pipe. Each note has a pipe, and the pipes get smaller as the pitch decreases. Remember that to go up an octave, you double the frequency and, in most cases, half the length of the thing that’s vibrating. Likewise down the octave is half the frequency and double the pipe length.
The 16ft rank is double the length, the octave below. Typically you will find 16 ft, 8ft, 4ft. In larger places, 32ft and 64 foot, the really really large ones, are almost inaudible at the lower end.
One really inescapable thing about pipe organs is that each rank takes up more space as you keep adding more. The really cool thing about computers is that you they don’t.
We’re going to modify our program. I’m going to make 5 oscillators. I’m going to use Sine waves because that’s close to a standard diapason stop on an organ. I can use an array to store them thus.
SinOsc osc[5];
osc[0] => dac;
osc[1] => dac;
osc[2] => dac;
osc[3] => dac;
osc[4] => dac;
I could have looped over to connect them to the dac if I’d wanted. But I didn’t. This will allow me to comment out lines so I connect or disconnect my oscillators. I can then play around with them to get an interesting sound like I might with organ stops, until I’m thrown out of the church.
Next I’m going to create a function which takes a frequency as a parameter. It will assign a quarter of the frequency to the first oscillator, half the frequency to the next and so on. Note the constructive use of comments.
function void setFrequency(float f)
{
f / 4 => osc[0].freq; // 64ft
f / 2 => osc[1].freq; // 32ft
f * 1 => osc[2].freq; // 8ft
f * 2 => osc[3].freq; // 4ft
f * 4 => osc[4].freq; // 2ft
}
The return type of the function is void, because it doesn’t have any information to give back to me. I can then call that function in my loop. This makes for a more convincing organ sound than I thought it would.
Here is the complete code. Try it out. Comment out various dac assignments with a // at the start of the line. Again, you won’t hear five oscillators, you will hear a timbre. Isn’t that cool.
int D, E, F, Fs, G, A, B, c, d, e, f, fs, g, a, b;
62 => D;
64 => E;
65 => F;
66 => Fs;
67 => G;
69 => A;
71 => B;
72 => c;
74 => d;
76 => e;
77 => f;
78 => fs;
79 => g;
81 => a;
83 => b;
int pitches[];
[G,A, B,d,c, c,e,d,d,g,fs, g,d,B, G,A,B,c,d,e, d,c,B, A,B,G,Fs,G,A, D,Fs,A, c,B,A,B,G,A, B,d,c, c,e,d, d,g,fs, g,d,B, G,A,B, A,d,c, B,A,G, D,G,Fs, G,B,d, g,d,B, G] @=> pitches;
SinOsc osc[5];
osc[0] => dac;
osc[1] => dac;
osc[2] => dac;
osc[3] => dac;
osc[4] => dac;
function void setFrequency(float f)
{
f / 4=> osc[0].freq;
f / 2 => osc[1].freq;
f * 1 => osc[2].freq;
f * 2 => osc[3].freq;
f * 4 => osc[4].freq;
}
int length;
pitches.size() => length;
int i;
for (0 => i; i < length; i+1 => i)
{
float frequency;
Std.mtof(pitches[i]) => frequency;
setFrequency(frequency);
0.25 :: second => now;
}
Thanks for reading.