This is number 2 in my series of lectures in music technology and ChucK to the Oxford Laptop Orchestra. Give the first lecture a read before reading this.
Last week we took a look at why, in my opinion, music and programming are natural bedfellows. We talked about what a program actually is and how it relates to Western music notation. We compared structural features of music and computer programs. We pinned down what the words ‘analogue’ and ‘digital’ actually mean, how sound is transmitted, and finally we wrote a program that plays a tune.
This week we’re going to continue down two parallel paths: more about the programming language and the nature of sound in general. The reason for all of this is to give you the tools to think about what you hear, apply analytical thought to the process of composition and creation, and to enable you to conceive of and make your own ChucK sounds.
Lecture 2 : Control Structures and Timbres
Repetition vs Loops
Last week we made a function, which was useful because it meant we could package up a series of instructions. We then said ‘call this function twice’, and lo and behold it was executed twice.
We’re going to write our repeated sequence of notes in a slightly more conventional way now.

What does this mean?
- Remember the barline, because we’re going to have to jump back to it.
- Play the notes.
- Jump back to the first barline and keep playing.
- Ignore the close-repeat-bar second time round.
Those repeat bars surround a block of instructions (notes). They mean here’s a sequence of instructions and I want you to do this twice. We were packaging the concept of this sequence of notes up in a function, but we weren’t really expressing play it twice very accurately as a concept. We were saying play it, then play it again, which is slightly different. If we wanted to play it 100 times we’d have to call the function 100 times. And that’s a bad thing, when you could have just typed the number ‘100’ in somewhere.
Loops
This is what we call a loop. In the broadest sense, a loop means do something a number of times. They’re pretty important in programming. Any time you see a series of things being acted on in series or as a group, which is basically everything, a loop is being used.
There are two parts to a loop. The first is some kind of decision making process, the second is the instructions that should be executed.
You’ll remember that a variable is a label which is used to store a value. We can create a variable to represent the number of times we’ve gone round a loop, adding one to it each time, and stopping when it reaches a certain number. Here I’m going to introduce a new bit of ChucK: the for loop. It’s called a for loop because the syntax starts with a condition that must hold true. ‘For the following condition, do this’. It has to be called something.
One convention that has been with us for at least 50 years (page 20 of this manual) is giving the name i to the variable we’re going to use to count. We’re going to use a few bits of ChucK syntax.
int i;
This means ‘create a variable of type integer called i’.
0 => i;
This means take the value zero, and assign it to i.
i + 1 => i;
This means take the value of i, add one to it, and assign it back to _i. _In other words, increase the value of i by 1.
Finally, this:
i < 10
This means ‘is i less than 10?’. It’s an expression, and the result can be true or false, depending on what the value of i is.
Let’s introduce the for loop. It has three clauses, in brackets.
for («thing to do before first repetition»; «condition»; «thing to run after each repetition»)
Each clause is separated by semi-colons. The first one is a statement that executes before the block of code that’s connected to the loop, runs. The second one is a condition that must hold true in order for the loop to keep executing. The third one is a statement that is run after each repetition. The loop keeps running until the expression is no longer true, and then continues with the rest of the program. If we plumb in the above, we get:
int i;
for (0 => i; i < 10; i + 1 => i)
Hopefully this makes sense in the light of the above. You can read this as ‘run this loop 10 times’. Each repetition of the loop, i will have the value of 0, 1, 2, 3, 4, 5 , 6, 7, 8, 9. The last time round, i will be incremented to the value of 10, but because it will no longer be true that i < 10, the loop will stop repeating.
Like a function, a loop takes a block of code to run, sandwiched between two braces, a { and a }.
Here’s last week’s example rehashed to use a for loop instead of a function. Unlike a function (which is a way of storing code for later), the computer will execute the for loop as soon as it sees it. Here is a complete program that performs our piece of music.
SinOsc myOscillator;
myOscillator => dac;
int d;
293 => d;
int e;
329 => e;
int fs;
369 => fs;
int g;
391 => g;
int a;
440 => a;
dur quaver;
0.5::second => quaver;
dur crotchet;
quaver * 2 => crotchet;
int i;
for (0 => i; i < 2; i + 1 => i)
{
d => myOscillator.freq;
quaver => now;
e => myOscillator.freq;
quaver => now;
fs => myOscillator.freq;
quaver => now;
g => myOscillator.freq;
quaver => now;
a => myOscillator.freq;
crotchet => now;
}
Why does a violin sound like a violin?
We used a sine wave oscillator last week. A sine wave is the purest kind of wave. It holds special mathematical status as the building-block of all sounds. We’ll look at that in detail later.
If you attach a weight to a perfect spring and drop it, the movement up and down will be a sine wave, albeit a slow one that you can’t hear. Our violin is a bit like this, inasmuch as it’s springy and bounces back and forward. But it doesn’t make a sine wave.
There’s no p in string
This is for all kinds of reasons. Chief amongst these is that it’s not actually equivalent to that spring. A string will vibrate at a number of frequencies at the same time. These are known as harmonics or overtones. All orchestral instrument players will know about these, with the possible exception of piano players. A violinist knows how to stop a string in a certain place in order to suppress certain frequencies and bring out harmonics. A flute player knows how to over-blow to get a second octave. A brass player knows how to change their embouchure to force the tube to vibrate at whatever harmonic they want. A harp player knows the best place to pluck the string. A piano player just hits the piano keys and hope something nice comes out. They can, however ask a violin player to show them, violin players are usually good natured.
So a resonant chamber resonates not only at its loudest frequency, called the fundamental, but also at various multiples of it. They’re generally always present, but you can, depending on the instrument emphasise some over others, or remove them altogether.
There is a strict mathematical formula to the harmonic sequence, and instruments will be characterised by the harmonics that they emphasise. They also produce a lot of other frequencies alongside. The combination of frequencies is defined by the construction of an instrument, and they are what produces the individual timbre of an instrument. The timbre can be described purely as the set of frequencies that an instrument makes when bowed / plucked / hit / dropped.
Oh yeah? Prove it.
If you’d been in the lecture you would have witnessed me trying to play a French horn, a recorder and a piano. Not all at once. We listened to the sound, looked at the waveform and also looked at the spectrogram.
Happily these recordings are confined to history. There’s nothing to stop you having a go.
Synthesis
Synthesis is the process of creating a desired sound from scratch. Synthesisers have been used to create all kinds of crazy sounds over the years. The earliest users of synthesisers were so overjoyed that these shiny new machines actually existed that the sheer power of their exuberance led to some quite alarming, unnatural if innovative, sounds. Over the years people have tried to create exciting new sounds as well as try to reproduce sounds that existed before synthesisers.
More or less
There are two kinds of synthesisers. Three if you count samplers, which re-play a pre-existing recording, but we’re not counting them today. We know that all musical sounds can, in theory, be built up by by adding together sine waves. Doing this is called additive synthesis, as we’re adding signals together in the aim of producing the sound we want. We also have subtractive synthesis, which means starting with a sound, containing a large number of frequencies, and filtering out the ones we don’t want. Most synths are a combination of the two. We’re talking about Moogs, and the kind of synthy sounds you’d hear in the 70s, 80s and 90s here.
Imagine trying to synthesise the sound of a real instrument from scratch. A quick look at the spectrogram revels that even our simple sound contains a large number of frequencies. These early synthesisers (in fact, all analogue synthesisers) needed a seaprate oscillator for every frequency they wanted to generate, so naturally additive synthesis of sine waves to reproduce a natural sound wasn’t a particularly popular or cheap way of doing things.
Adding random sines
It’s actually a very subtle and difficult process to try and model a real instrument with sine waves. I’ve written a small chuck program to take 200 sine waves, at random frequencies, and play them at once. Don’t worry about the syntax, but do worry about how it sounds and the spectrogram.
SinOsc oscs[200];
for (0 => int x; x < oscs.size(); x++)
{
Std.rand2f(100.0, 10000.0) => oscs[x].freq;
Std.rand2f(0.0, 0.05) => oscs[x].gain;
}
for (0 => int x; x < oscs.size(); x++)
{
0.1 :: second => now;
oscs[x] => dac;
}
5::second => now;
This layers the up, one at a time, until it gets to 200. You can run this several times and get different sounds. Here’s a trial run:
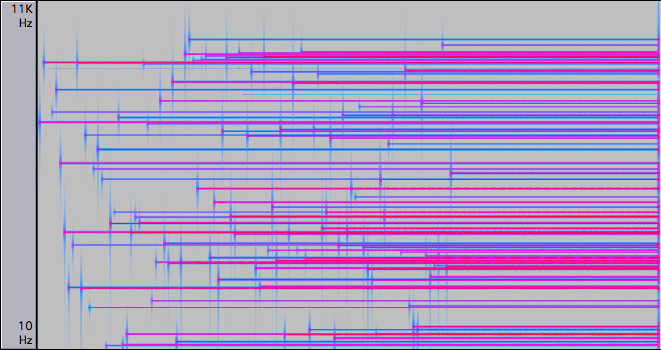
It sounds very odd because the random numbers have no mathematical relationship with each other. The closest thing you can probably think of is a cymbal, which makes all kinds of random frequencies when you suddenly inject a huge amount of energy and the metal is trying to work out what the hell to do with it.
Adding not-random sines
Here’s another ChucK program. It has 20 oscillators, each is a multiple of 200 (so the values are 200 * 1, 200 * 2, 200 * 3 etc). The amplitude of each frequency is also decreased as we get higher. Brass players will recognise the harmonic sequence as they are exposed to it every day.
SinOsc oscs[20];
for (0 => int x; x < oscs.size(); x++)
{
200 * (x + 1) => oscs[x].freq;
1.0 / (x + 1) => oscs[x].gain;
}
for (0 => int x; x < oscs.size(); x++)
{
0.5 :: second => now;
oscs[x] => dac;
}
5::second => now;
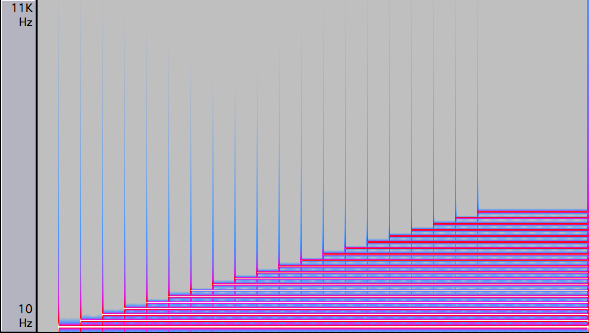
Here are two recordings. The first plays only one frequency at once. Any brass player can make a tube do this, albeit only up three or four harmonics.
The second recording plays them all at once, as per the above spectrogram.
Notice that it sounds more like a musical note, but becomes less pleasant the more harmonics we add. But it does sound musical, where the random ones really didn’t.
Just for fun I sped up the rate that it adds sine waves (such that the whole progression took 0.2 seconds). Look at the changing shape of the wave. Think about the timbre. Remember it for a couple of minutes' time.

Meet the Family
Of course, sine waves aren’t the only signal we can start with. I’m going to introduce you to four characters, the usual suspects of music synthesis. They were popular because they sounded interesting, and building an electronic circuit to make these signals wasn’t hard. We’re also going to be thinking about the shape of the wave and how it sounds. It is possible to look at certain sound waves and get a rough picture of how they sound.
First up, we have the sine wave, with whom we are well acquainted by now.

As with all waves, it moves between one peak and the other. The point at which it turns around at the top or bottom are quite gentle: it’s a careful driver when it comes to taking its corners. It moves fairly quickly when it’s crossing zero, but it doesn’t have any sudden accelleration or decelleration.
It sounds ‘soft’. It’s difficult to describe the sine wave, because it’s the building-block for describing other waves. It’s exactly one frequency, so it’s very focussed. ‘Soft and inoffensive, but intense’ are the only words I can really think of. Maybe you can come up with better words. The sine wave is the only wave that we can say contains only one frequency.
Next up we have the triangle wave.

It moves from one extreme to the other like the sine wave, but turns around rather abruptly at the extremes. It’s smooth most of the time, but certainly has a ‘point’. It has the same kind of sound as a sine wave but has a bit of an edge to it. That edge in the sound you can hear is actually the sharp corner believe it or not.
Next, we’re going to go to the extreme.

The square wave crosses straight from one one extreme to the other. This square edge sounds brutal. It’s a horrible sound. It’s the easiest to make from an electronics standpoint, as you’re just turning a switch on and off. It’s not very nice to listen to, because of those square edges.
Finally, the saw tooth wave.

It is so named because it is a kind of wave, and it resembles the teeth of a saw. It combines the sharp edge of the square wave with the triangular slope of the triangle wave. You’ll be able to hear some similarities I hope.
Now let’s look at the frequency content.
The sine wave is uncontraversial. It contains one frequency.

The triangle wave is the next simplest. It has a smattering of frequencies at regular intervals.

Next up square.
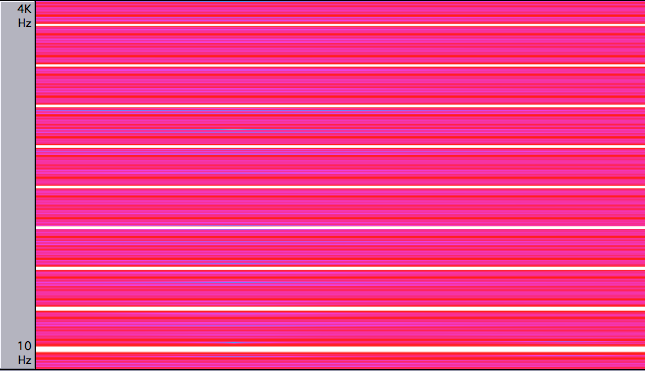
Finally, the sawtooth
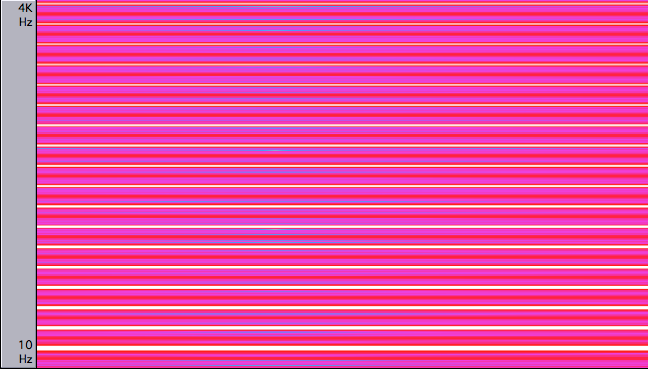
A lot more frequencies, a lot closer together. But the last three all contain the harmonic series, those present in the triangle. Of course, it’s not the number of frequencies that make something sound pleaseant or unpleasant, it’s the selection of them.
DIY
I encourage you to engage in some critical listening. You might study a Bach piece for counterpoint. Why not do the same for frequency content and timbre? Grab a copy of Audacity (it’s free and open source), make your own recordings, or listen to some MP3s, and think about the frequency content and how they sound.
Sine waves aren’t much fun to listen to. Let’s change our piece of music to use different oscillators. ChucK has the following oscillators (amongst others) built-in:
SinOsc mySinewaveOscillator;
SawOsc mySawtoothOscillator;
TriOsc myTriangleOscaillator;
SqrOsc mySquareWaveOscillator;
Try plumbing in our oscillators into our marvellous piece of music. Have a play with these yourself during the week. Choose your favourite.
No buts. Some ifs.
Running the danger of making our piece of music too exciting, we’re going to add first- and second-time bars.

Let’s break out into boring-mode again and describe this.
- Remember this point, we’re going to have to repeat. Also remember how many times we’ve repeated.
- Play up to the repeat symbol.
- If there’s a bar with the same label as the number of times you’ve repeated, play it.
- If there’s a close-repeat mark, jump to the start.
- If not, continue.
So if we can cast our mind back to last week, the two important concepts in programming, as in interpretive dance, here are:
- Jumping around
- Taking a decision
We know about for loops, and we know that we can use them to count between two numbers. We just need to be able to take a decision based on the value of the variable, which we’ve called i (but could be called anything). You should be getting the hang of braces to {enclose statements} by now. If you haven’t, take it on trust for a bit longer, it’ll sink in I promise.
The statement to evaluate a decision is somewhat uncontravertially called if, and it takes as a parameter an expression which evaluates to true or false.
One other bit of syntax is ‘equals’, and in ChucK it’s spelled ‘==’.
I’m going to dive right in here and implement our new tune.
SawOsc myOscillator;
myOscillator => dac;
293 => int d;
329 => int e;
369 => int fs;
391 => int g;
440 => int a;
dur quaver;
1::minute / 200 => quaver;
int i;
for (0 => i; i < 2; i + 1 => i)
{
d => myOscillator.freq;
quaver => now;
e => myOscillator.freq;
quaver => now;
fs => myOscillator.freq;
quaver => now;
g => myOscillator.freq;
quaver => now;
a => myOscillator.freq;
quaver * 2 => now;
if (i == 0)
{
a => myOscillator.freq;
quaver => now;
fs => myOscillator.freq;
quaver => now;
d => myOscillator.freq;
quaver => now;
fs => myOscillator.freq;
quaver => now;
a => myOscillator.freq;
quaver * 2 => now;
}
if (i == 1)
{
a => myOscillator.freq;
quaver => now;
d => myOscillator.freq;
quaver => now;
d => myOscillator.freq;
quaver => now;
fs => myOscillator.freq;
quaver => now;
d => myOscillator.freq;
quaver * 2 => now;
}
}
- This will perform the loop once with i having a value of zero.
- The test of the first if statement is that i is zero, which is true, so it executes the statements inside the braces.
- It then reaches the second if, which is not true, so it ignores the contents of the braces.
- It then adds one to the value of i, and plays the contents of the for loop again, because i is less than 2.
- It runs the contents of the braces, comes to the first if statement which is no longer true, so skips over it and comes to the second if statement, which is now true, so it executes it.
- It then increments the value of i (now it’s 2), performs the for loop test. It is no longer true that i is smaller than 2, so it doesn’t loop again.
- Control reaches the end of the program, so it exits.
That’s an if statement.
BONUS MATERIAL
Not covered in the lecture, I will do next time round.
MIDI
Finally we’re going to touch on MIDI. MIDI stands for Musical Instrument digita Interface. It’s a way of encoding musical instructions as a sequence of bytes. This can be sent down a cable, or can be stored in a file. It was devised in the 80s and it marked an interesting transition between analogue and digital.
A synthesiser has various parameters. The most important ones are frequency and amplitude. As more synths started appearing, and more ways to play them (usually keyboards) a standard was needed. Previoulsy these parameters were controlled by a ‘control voltage’ which was an analogue signal, usually between zero and 1 volts. A keyboard would create a high voltage for a high note, and a low voltage for a low note. But the meaning of voltage varied from machine to machine. A digital standard was needed.
I can go into any amount of depth about MIDI if you want, but for now I’m just making you aware of it. They standardised on a way of describing pitches, on a scale of 0 to 127, with 60 being middle C and each increasing number corresponding to a semitone. So if middle Middle C is 60, the C above it is 72.
Real functions returns
We wrote a function last week. It was just a block of code. But if you’ve ever talked about functions before in maths, you’ll be talking about something that takes an input and gives an output. You might have a function called multiply by two which takes an input number and returns back to you a number. It may perform any amount of processing to get to that point, but it fundamentally takes arguments and returns something. It can also take any number of inputs, not just one.
Null and void
Lucky for us, one of the kinds of thing it can return is ‘nothing’, called ‘void’. And ‘any number’ can be zero. The function we wrote last week took no parameters (aka arguments) and returned no value.
The value of music
There is an equation for working out the frequency of a note if you know the pitch. It’s not really reasonable to have to know (or work out) the frequencies of the notes you want to use, but it is reasonable to know the MIDI pitch, you can work it out easily. I’m going to clean up our source code a bit by removing frequencies and instead writing MIDI pitch numbers.
We still need to know the equation to turn that into a frequency, but lucky for us there is a function built into ChucK which will do that for us. It’s a function that takes a number as an input (the pitch number) and returns a number, which is the frequency. We can use the returned value from a function and assign it to the freq of an oscillator. I’m going to use this in a simplified version of our program.
TriOsc myOscillator;
myOscillator => dac;
62 => int d;
64 => int e;
66 => int fs;
67 => int g;
69 => int a;
dur quaver;
1::minute / 200 => quaver;
Std.mtof(d) => myOscillator.freq;
quaver => now;
Std.mtof(e) => myOscillator.freq;
quaver => now;
Std.mtof(fs) => myOscillator.freq;
quaver => now;
Std.mtof(g) => myOscillator.freq;
quaver => now;
Std.mtof(a) => myOscillator.freq;
quaver * 2 => now;
This looks a little unweildy, but the point I’m demostrating here is that you can call a function and use its return value in the same way as you could use a variable or a just a literal number.
Fin.
That’s it for this week. You should now be masters of for loops, basic waveforms, if statements, and a bit more clued up about MIDI. Thank you and goodnight.